化学のまとめ
アルデヒド
アルデヒドはカルボニル炭素に水素原子が一つ置換した構造を持つ有機化合物。一般式は$\rm{R-CHO}$。RもHのときがホルムアルデヒド。Rがメチル基だとエタナールまたはエチルアルデヒド、そして通称アセトアルデヒド。
ケトン
ケトンは一般式$\rm{R−C(=O)−R'}$で表される構造を持つ有機化合物。R、R'ともにメチル基の時がアセトンまたはプロパノンである。
エーテル
エーテルは一般式$\rm R−O−R'$で表される構造を持つ有機化合物である。$\rm -O-$をエーテル結合という。
エノール
エノールはアルケンの二重結合炭素の片方の炭素にヒドロキシ基が結合したアルコール。ただし非常に不安定ですぐにケト-エノール互変異性を起こしてケトンになる。
エステル
エステルは、有機酸または無機酸のオキソ酸とアルコールまたはフェノールのようなヒドロキシル基を含む化合物との縮合反応で得られる化合物。
エポキシド
エポキシドは3員環のエーテルであるオキサシクロプロパン(オキシラン)を持つ化合物。$sp^3$混成軌道は結合角が109.5°だが図の通り60°で結合しているのでとにかく不安定。そのため反応性が高く、簡単に開裂する。
アルコキシド
アルコキシドはアルコールの共役塩基であるアニオンのこと。共役塩基の説明は別項参照。ようするにアルコールの$\rm OH$から$\rm H^+$が脱離し$\rm O^-$となったもの。
フェノキシドフェノキシドはフェノール類の共役塩基のこと。ようはアルコキシドのRが芳香族のときがフェノキシド
共役酸・共役塩基物質から水素イオンがひとつ付加したものをその物質の共役酸という。逆に水素イオンがひとつ脱離したものを共役塩基という。
ジカルボン酸・トリカルボン酸ジカルボン酸はカルボキシル基$\rm COOH$を2つ持つもの。$\rm R$を挟むように2つのカルボキシル基が出ている。カルボキシル基が3つあるとトリカルボン酸となる。
酸・塩基・アレニウスの定義
水$\rm H_2O$に解けたとき、$\rm H^+$の濃度を高めるものを酸、$\rm OH^-$の濃度を高めるものを塩基という。
・ブレンステッド・ローリーの定義
$\rm H^+$を与えるものが酸、$\rm H^+$を受け取るものが塩基という。
・ルイスの定義
電子対を受け取るものが酸、電子対を供与するものが塩基という。
酸化還元反応酸化還元反応とは電子の授受がある反応のこと。酸化と還元は同時に起こる。
酸化=電子を失う(水素原子を失う・酸素原子を受け取る)
還元=電子を受け取る(水素原子を受け取る・酸素原子を失う)
酸化剤=相手を酸化するので自分は還元される
還元剤=相手を還元するので自分は酸化される
酸化剤・還元剤はあくまで相手との関係で決まるものなので、一般に酸化剤と言われる物質でも相手の物質によっては還元剤として働くこともある。
酸化数のまとめPDFリンク
$\rm pH$・$pK_a$・$K_a$化学における$\log$は底が10の常用対数のことをいう。数学では単純に$\log$といえば底がeの自然対数$
\rm ln$をいうので数学寄りの人間は注意。
$${\rm pH} = - \log[H^+]$$
$$K_a = \rm \frac{[A^-][H^+]}{[AH]}$$
$$ pK_a = - \log K_a $$
$$ {\rm pH} = pK_a + \rm \log \frac{[A^-]}{[AH]} $$
$$ \frac{K_a}{\rm [H^+]} = \rm \frac{[A^-]}{[AH]} $$
緩衝能は$pK_a$と$\rm pH$が近い程大きくなる。また、${\rm pH} = pK_a$のとき酸$\rm HA$は50%解離する。
また、$pX$という変数が意味するものは$pX = - \log X$。
VSEPR(原子価殻電子対反発)理論電子対間の反発の強さは次の順になる
(結合電子対$-$結合電子対) $<$ (結合電子対$-$非共有電子対) $<$ (非共有電子対$-$非共有電子対)
例えば$\rm H^2O$はe結合電子対2つ、非共有電子対2つである。本来それぞれの電子対はクーロンの法則に従い、お互いに等しい力を及ぼし合う正四面体の頂点に位置するよう配置される。しかし結合電子対と非共有電子対とで反発の度合いが違う。上に書いた順番が示すのは非共有電子対はよく反発し、結果として多くの空間を専有するということ。よって共有電子対は非共有電子対に押され狭い空間へ、つまり角度が小さくなる。正四面体の頂点に来る場合は109.5°だがそれよりも小さい104.5°になる。
| $n$ | 分子形 | 混成 | 分子例 |
| 2 | 直線型 | $\rm sp$ | $\rm BeCl_3$ |
| 3 | 平面三角形型 | $\rm sp^2$ | $\rm BCl_3$ |
| 4 | 正四面体型 | $\rm sp^3$ | $\rm CH_4$ |
| 平面正方形型 | $\rm dsp^2$ | $\rm [Cu(NH_3)_4]^{+2}$ |
| 5 | 三方両錐型 | $\rm dsp^3$ | $\rm PCl_5$ |
| 6 | 正八面体型 | $\rm d^2sp^3$ | $\rm SF_6$ |
| 7 | 五方両錐型 | $\rm d^3sp^3$ | $\rm IF_7$ |
| 8 | 正十二面体型 | $\rm d^4sp^3$ | $\rm [Mo(CN)_8]^{4-}$ |
軌道のs性混成軌道においてs軌道の占める割合がs性である。s性は次の通りになる。
$sp$混成軌道=50%
$sp^2$混成軌道=33%
$sp^3$混成軌道=25%
s軌道は原子に近いのでs性が高いほど安定となる。
フィッシャー投影式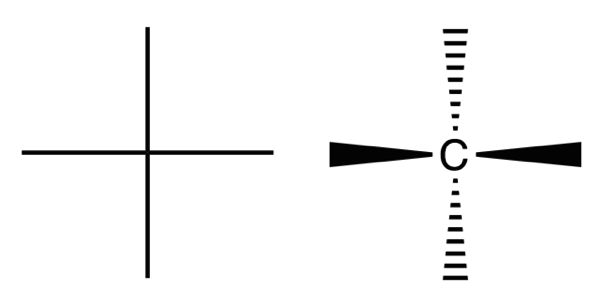
左がフィッシャー投影式で右がその実際の意味を示した図。右は破線-くさび形記法で塗りつぶしが手前、破線が奥に伸びていることを示す。
元素の性質定義
・イオン化エネルギー:大きいほど陽イオンになりにくい
・電気親和力:大きいほど陰イオンになりやすい
・電気陰性度:小さいほど陽イオンになりやすく大きいほど陰イオンなりやすい
また、第一イオン化エネルギーと第二イオン化エネルギーがある。
・第一イオン化エネルギー:電子を一つ取り去って1価の陽イオンにするとき
・第二イオン化エネルギー:1価の陽イオンから2価の陽イオンにするとき
周期律
周期表右上に行くほど
・イオン化エネルギー:増大傾向にあるが多少変動あり
・電気陰性度:増大傾向にあるが多少変動あり
・電気陰性度:きれいに増大する
希ガスはイオン化エネルギーが大きく、また電気親和力も小さい(出しにくく奪いにくい)。
分子の極性共有電子対は電気陰性度が大きい原子に引き寄せられ、分子に極性が現れる。
よくでる原子の電気陰性度。ポーリングの電気陰性度では希ガスの値はなし。
O 3.4
Cl 3.2
N 3.0
C 2.6
H 2.2
第二族Li~Fは順に電気陰性度が大きくなり、BとCの間にHが入る。ClはNとOの間に入る。
原子の大きさ原子の大きさは
・同一周期では左に行くほど大きい
・同一族では下に行くほど大きい
二量体
二量体とは分子が2つ結合したもの。共有結合や水素結合などで結合している。カルボン酸は$\rm OH$と$\rm CO$が水素結合している。図はカルボン酸の二量体。水も水素結合して二量体を形成している。
結合力の比較共有結合を100としたとき
共有結合100 > 水素結合10 > ファンデルワールス力1
スレーターの規則有効核電荷を$Z^*$、陽子数を$Z$、遮蔽定数を$S$とすると
\begin{align}
Z^* = Z - S
\end{align}
となる。
原子$^A_ZX$
$Z$が陽子数(原子番号)で$A$が質量数。よって中性子数$N=A-Z$となる。
同位体 $Z$が等しく$N$が異なる核。つまり同じ原子番号で質量数が異なるもの。
周期表1から18族まである。18族(希ガス)の元素はHeを除いてp軌道まで埋めて閉殻構造となる。これは軌道のエネルギーが数字通りでないため。例えば第5周期の希ガスXeは6p軌道まで埋める。第6周期は7s軌道から始める。ランタノイドとアクチノイドは15個ずつ。
典型元素は1族2族と12族から18族で遷移元素は3から11族まで。4周期目から割り込む3から12族のうち12族だけ典型元素なので注意。
| 主殻 | 副殻 |
| K | 1s |
| L | 2s, 2p |
| M | 3s, 3p, 3d |
| N | 4s, 4p, 4d, 4f |
| O | 5s, 5p, 5d, 5f |
| P | 6s, 6p, 6d |
| Q | 7s, 7p |
ちなみに右上から左下に辿る順にエネルギーが高くなる。例えば3pの次は3dではなく左下の4sへ続く。4sは左下がないので3dへ戻りそこからまた左下へとたどっていく。
$\alpha, \beta, \gamma$崩壊$\alpha$崩壊とはアルファ粒子を放出する放射性崩壊。アルファ粒子とは陽子2つ中性子2つ、つまりHe原子核のこと。式で表せば$\rm _2^4He^{2+}$。アルファ崩壊が起きると原子番号と中性子が2つずつ減り、質量としては4減る。
$\beta$崩壊とは原子核の中性子が電子を1つ放出し陽子へ変化する放射性崩壊。質量は変わらないが原子番号が増える。ちなみにこのときニュートリノも放出されている。
$\gamma$崩壊とは励起された原子核がガンマ線を放出する放射性崩壊。ガンマ線とは波長が10pmよりも短い電磁波である。$\gamma$崩壊は核種が変わらない。
量子数$n$:主量子数($n=1,2,3,...$)→K,L,M,N...殻を決定する
$l$:方位量子数($l=0,1,...,n-1$)(軌道角運動量量子数)→s,p,d,fなど軌道を決定する
$m_l$:磁気量子数($m_l=0,1,...,\pm l$ )(軌道磁気量子数)→$p_x,p_y,p_z$などを決定する
$m_s$:スピン磁気量子数→スピンの向きを決定する
これら4つの量子数により電子の量子状態$(n,\ l,\ l_m,\ l_s)$が決定する。また、同一の量子状態をとることができない。これをパウリの排他原理という。また、同じエネルギー準位であれば別々の軌道($m_l$が異なる)にスピン磁気量子数$m_s$を揃えながら入る。これをフントの規則という。
光電効果光電効果で重要なのは、ある一定の振動数$\nu_0$以上与えた時に光電子が飛び出たならばそれよりも低い振動数では光の強さを強くしようが光電子は飛び出さない。逆にそれよりも高い振動数であればどんなに弱い光でも飛び出す。光子のエネルギーは振動数のみによって決定される。ちなみに光の強度とは光子の数のこと。
仕事関数$W$は金属中から電子1個を取り出すのに必要な最小のエネルギーを意味する。正確には真空中に取り出すときのエネルギーである。
分子の衝突まず衝突断面積というものを定義する。これは2つの分子(ここでは球形であるとした場合)の半径の和を半径とする円の面積。これはこの円の中心に分子Aを置いた時、もう一つの分子Bが衝突する範囲である。この円の中に分子Bの中心があれば衝突する。よって衝突の頻度は
$$ \overline{v_a} \times 衝突断面積 \times Bの濃度 $$
つまり分子Aが単位時間あたりに進む間に衝突範囲内にある分子Bの数である。
ファンデルワールスの状態方程式\begin{align}
\left( P + \frac{n^2a}{V^2} \right)(V - nb) = nRT
\end{align}
aは分子間力の係数でbが自身の体積による影響の係数。これらは分子の大きさなどによって個別に決まる。
標準電極電位とギブスの自由エネルギー標準電極電位$E^0$とギブスの自由エネルギーの変化量$\varDelta G$の関係式は
$$\varDelta = -nFE^0$$
となる。ここで$F$はファラデー定数で$n$は電子にかかる係数。$\varDelta G<0$のとき反応は自然と進行する。




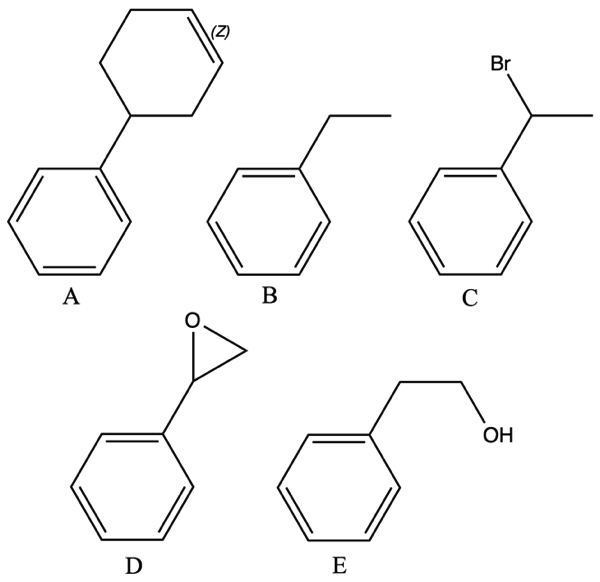





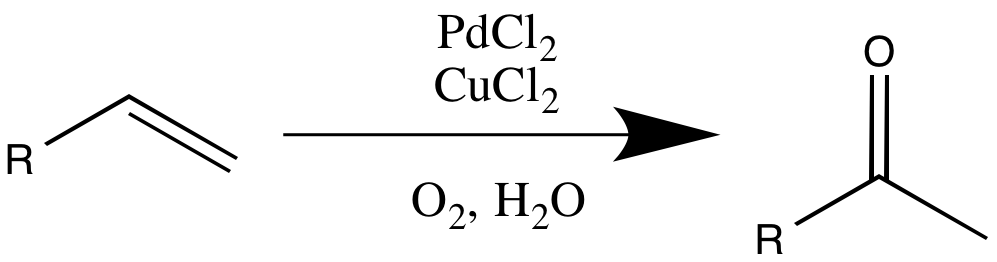
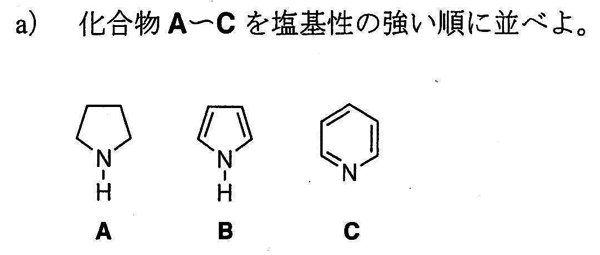












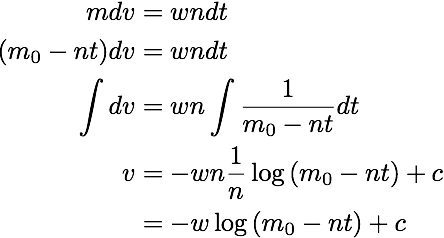



 初期条件を求めてまとめると
初期条件を求めてまとめると