図のように、長さlの糸の先に質量mの物体を取り付け初速度V0で打ち出す。このとき、
(1)糸がたるまずに振動するためのV0
(2)糸がたるまずに回転するためのV0
を求めよ。
(1)
まず張力Tを求める。
張力Tは物体の遠心力と重力の法線成分の和とつりあっている。
また、力学的エネルギー保存則により次の式が立つ。

左辺がt=0での力学的エネルギー、右辺が角度θのときの力学的エネルギーである。物体が折り返すときはv=0のときであるから、次のように変形してv=0のときの角度を求める。
これを最初に立てた張力の式に代入する。物体が折り返すとき、例によってv=0なので遠心力は0となり、また張力が0以上であればたるまない。よって
以上のように求まる。結局これは折り返すときに遠心力が働かないので、張力を作り出しているのは重力だけだということがポイントである。なので回転角は90°までになる。
(2)
今度は物体が頂上まで来た時に張力が0以上であればよい。頂上ということはθ=πなのでこれを(1)で求めた式に代入してv0を求める。
張力の式にθ=πを代入すると
同様に力学的エネルギー保存則の式にも代入すると
これを張力の式に当てはめれば求まる。
ようは頂点での速度を初速度を用いて表し、これを張力の式に当てはめればその時の張力がわかる。あとはこの張力がたるまないという条件に沿うよう初速度を設定すればよい。




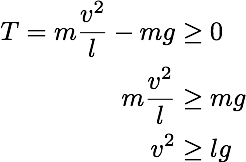


0 件のコメント:
コメントを投稿