ロケットの打ち上げの問題で悩んだので整理してまとめておく。 ちなみにこの問題の結論となる式はツィオルコフスキーの公式と呼ばれている(ロシアのツィオルコフスキーが考えたので)。
まず、僕が思うスタンダードな解き方。 ロケットの時刻tにおける速度をv、tにおけるロケットの質量をm、ガスの時間あたりの噴射量をn、ガスの噴射速度をwとする。
運動量保存則に従って式を立てる。左辺が時刻tでの運動量で右辺がt+Δtでの運動量である。
右辺第1項がロケットの運動量、第2項が噴射されたガスの運動量。ロケットはガスの分だけ軽くなりその分加速している。ガスは相対速度v-uで放出されている。
つぎにこの式の括弧を展開する。このとき微小量の2次の項は無視しても構わないことに注意。展開して微小量の2次の項を消すと次のようになる。
ここでロケットの時刻tにおける質量は次のようになるのでこれを代入する。
代入したものを計算していく。
初期条件t=0でv=0よりcを求め、まとめると
という結論が導かれる。 これは素直に運動量保存則の式を立てれば後は流れ作業で求まる。
では僕が悩んだのが次の解き方。といっても別に解き方が違うわけではなくガスの噴射量の変数の置き方が異なる場合の話。ガスの噴射量をさっきはn[kg/s]と置いたがそうではなく-Δmと置く場合である。とりあえずこの場合の運動量保存則の式を立てる。
見るからに違和感バリバリ。お陰で凄く悩まされた。 時刻が進むとロケットの質量が増加?ガスの分の運動量が引かれてるっておかしくないか?
ここで先ほどの
をもう一度見てみる。これをtで微分すると
これはつまり

こういうことなので、これを一番最初に立てた運動量保存則の式に当てはめると違和感バリバリの運動量保存則の式とおなじになる。 というわけで一見おかしいように見えて式自体は正しかったわけだ。
ではなぜあれで正しいのか。それはさっき求めたとおりΔmが負であるからだ。ようはこのΔmというのは単にガスの噴射量というわけではなくロケットの質量の変化量だということを思い出せばわかる。
単にΔmと書けば実際それが表すのは負の数である。だから実際の増えたり減ったりする質量としてみると正の数でなければいけないのでマイナスを付けている。
よってΔmを使った式を立てる場合は 以下のように考えて式を立てればよい。
一応この先の解き方を示しておく。例によってまず展開して微小量の2次の項を消去。
後は積分。

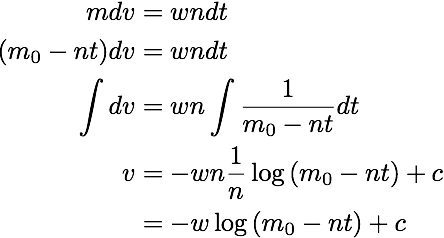


0 件のコメント:
コメントを投稿